Author:
Niek J. Bouman, PhD
CTO Roseman Labs
The topic of this document is privacy-preserving computation: computing on data, possibly originating from multiple data owners, in such way that neither the data owners nor the computing infrastructure(s) involved can ‘see’ data input by others, and such that the computational result is only revealed to those parties eligible to receive it. Privacy-preserving computation can add value by enabling data-driven collaborations based on sensitive data, and finds application in various domains, such as healthcare, financial services and public sector.
1. Scope
In this document we will distinguish between three flavours of privacy-preserving computation technologies, and for each technology we explain the basic idea, their primary use case and discuss their pros and cons: Trusted Execution Environments (TEEs), Fully Homomorphic Encryption (FHE) and Secure Multi-Party Computation (MPC). In fact, there is a fourth flavour of secure computation which is Functional Encryption (FE), which is promising but not yet mature; for an introduction into FE we refer to Wee (2014).
Some readers might expect to also read about Federated Learning (FL), which is often mentioned in the context of privacy-preserving data analysis. We do not discuss it here simply because Federated Learning does not guarantee data privacy by itself, since the publicly exchanged model parameters leak information about the underlying data. Instead, federated computation (of which FL is a special case) it is a computational paradigm, that can be made privacy-preserving by combining it with one of the above-mentioned technologies.
2. Defining Security
Before discussing the various technologies that we mentioned above in more detail, let us first ask the following question: What does it actually mean for privacy-preserving computation, or, a system in general, to be "secure"?
To answer this question, one should first precisely define the security properties that one would like the computation to have; we call this a security definition. In secure computation, it is typical to at least require correctness, meaning that the result of the computation will be correct, and privacy, namely that no party involved in the computation learns any information beyond the result of the computation, if that party is eligible to receive that result. In particular, each party should not be able to learn information on the inputs provided by others, except information about these inputs that can be deduced from the output. Note that there are some other common security properties in secure computation, like fairness or guaranteed output delivery, but we do not discuss those here.
We should also formally define the computation itself, by means of specifying the ideal functionality. We can imagine the ideal functionality as an “ideal” trusted party that receives inputs, performs the computation: for each party that is eligible to receive a result, the trusted party evaluates a (possibly different) function on the inputs, and sends back the results to the corresponding parties. The word “ideal” here means that the trusted party always computes correctly and is secure “by definition.” In the real world, the parties execute a protocol, which is essentially a recipe that specifies the sequence of computational steps and data-exchange steps that the parties should follow in order to jointly compute the final result.
Finally, we need to specify what type of adversary (the attacker) our computation should be secure against. The adversary is commonly imagined to be a single entity, which can corrupt one or more parties. One typically distinguishes between a semi-honest (also called “honest-but-curious”) adversary and a malicious (or active) adversary. In case of the former, all parties involved in the computation (including those corrupted by the adversary) follow the protocol, but try to learn as much information as possible from participating in the protocol. In case of the latter, the corrupted parties may deviate arbitrarily from the protocol description. We say that a protocol is passively secure if it is guaranteed to provide the security properties in the presence of a semi-honest adversary, and likewise, we say that a protocol is actively secure if its security properties hold in the presence of an active adversary.
2.1 Further Reading
For a more extensive treatment of defining security in secure computation, we recommend Pragmatic Introduction to Secure Multi-Party Computation by Evans et al., and How To Simulate It by Yehuda Lindell.
3. Trusted Execution Environments (or: Confidential Computing)
A trusted execution environment is a security technology, found inside certain microprocessors, that lets software applications define private regions of memory to store program code and/or data. The word ‘private’ means that those memory regions are encrypted at the processor level, such that the application itself can make normal use of those memory regions, while other applications and even the operating system cannot read data (and steal secrets!) from that memory in decrypted form. An important benefit of TEEs is that the performance of computation inside a TEE is in the same ballpark as ordinary computation on a CPU.
We can perform privacy-preserving computation using a TEE by treating the application that runs inside the TEE as a trusted party: parties send their inputs in encrypted form to the TEE, the TEE decrypts the data and processes it, and encrypts the result and sends it to the designated receiver(s).
Trusted-execution environment based computing is marketed under the name of “confidential computing”. Several processor vendors offer TEE technology; arguably the most well-known is Intel’s Software Guard eXtensions (SGX), while AMD, for example, offers a similar technology called Secure Memory Encryption (SME). The programming interfaces of the latter two technologies are different; meaning that an application written for Intel SGX cannot run on an AMD processor with SME, and vice versa. To mitigate this problem, there exist abstraction layers like the Open Enclave SDK (SDK stands for software development kit) that lets the programmer write an application that works with several underlying TEE technologies. Note that the feature sets of the major TEE technologies are not uniform, e.g., Intel SGX additionally supports a feature called ‘attestation’ with which you can convince another party about the presence of a genuine SGX- capable processor, and that some public key belongs to a private key that is tied to, and only known inside an SGX-TEE. Details of such features, however, are beyond the scope of this write up.
Certain cloud vendors offer compute nodes that specifically support TEE technology, like Microsoft’s “Azure Confidential Computing” and Google’s “Asylo” propositions.
3.1 TEE Software Development and Constant-Time Code
Because of the advent of high-quality SDKs, TEEs are relatively easy to use. Nonetheless, TEE-application-programmers should be careful to ensure that their code is “constant-time”, to avoid side channel leakage of secret information. Constant-timeness means that the software’s branching patterns (like if-else clauses), as well as the memory-access-patterns should be independent of secret information. (Actually, I personally prefer the term “secret-independence” over “constant-timeness”, as it captures the requirements more accurately.)
In case you are unfamiliar with the notion of constant time, then think, for example, of a software program that chooses among two actions based on a secret bit of information: if the bit is 0, the program performs a simple (and quick) computation; if the bit equals 1, the program performs a more involved and lengthier computation. Now, for some external observer, it is easy to learn the secret bit of information, simply by measuring the time the program takes to finish! Regarding the information leakage that can arise from memory-access-patterns, let us think of a program that accesses elements from an array A in memory, where at time k the xkth position of A is read, where x is some list of secret numbers. Because it is straightforward for some observer to figure out which memory location the processor is accessing at a given time, such a program would leak x via a memory-access-pattern side channel.
A personal observation from the author is that not every TEE-software developer is aware of this constant-time requirement. Hence, a perhaps surprising risk of the programmer-friendly TEE ecosystem is that non-experts can well succeed in building TEE-software that seems to behave correctly but is insecure due to side channels, ultimately leading to a false sense of security. In that sense, one could say that “don’t roll your own crypto” also applies to TEE-programming.
3.2 Security
One problem of TEEs is that their designs as well as their implementations are typically proprietary, which makes it hard to reason about the security properties of TEEs in a black-box sense (i.e., without looking into the details of the TEE implementation). Also, TEEs lack a rich academic theoretical-cryptography foundation (unlike FHE and MPC, which both have solid academic foundations). Both Intel and AMD’s TEE implementations have a poor track record with respect to security vulnerabilities; see, e.g. this paper by Randmets (2021) or simply search the web for vulnerabilities in Intel SGX or AMD SME. While some of those vulnerabilities can be patched via microcode updates, others can only be mitigated by physically replacing the processor. Although one could say that using a TEE will certainly make it (much) harder for an adversary to gain access to an application’s secrets than without using a TEE, but this might be too weak a guarantee, especially for high-security applications.
4. Fully Homomorphic Encryption
Fully homomorphic encryption (FHE) is a form of public-key encryption that enables us to perform arithmetic on encrypted values. (Recall that public-key encryption is an asymmetric form of encryption with which anyone knowing the public key can encrypt a message, but only the holder of the corresponding private key can decrypt the message.)
For concreteness, let’s take as example the addition of two integers a and b. We can always first add those integers to obtain the sum s := a + b, and then encrypt s with any public-key encryption scheme, to obtain a ciphertext cs (an encryption of s). The special feature of an (additively) homomorphic encryption scheme is that we can essentially exchange the order of encrypting and performing the addition: we first individually encrypt a and b, which gives respectively the ciphertexts ca and cb. Then, the homomorphic property of the encryption scheme admits the operation that takes two ciphertexts as input and returns an encryption of the sum of the underlying (unencrypted) values. Hence, when applying this operation to the pair (ca, cb), we obtain an encryption of s. Note that this ciphertext will practically never be identical to cs, which is in fact crucial for the security of the encryption scheme, but nonetheless both ciphertexts will decrypt to the same plaintext value.
A fully homomorphic encryption scheme admits not only the addition but also the multiplication of encrypted values. This is important, because addition and multiplication together form a so-called universal set of operations, with which any finite function can be computed, at least in principle.
Whilst the notion of fully homomorphic encryption exists since 1978, it took until 2009 before Craig Gentry proposed a construction (along with a mathematical security proof). Since then, there have been many improvements; we refer the interested reader to the Wikipedia article about homomorphic encryption.
The classical use case for FHE is computation delegation: suppose you want to delegate a computation on sensitive data to some Cloud service (e.g., because you do not have enough computational resources yourself), but you do not want the Cloud to learn your sensitive input data. To achieve this using FHE, you would encrypt (before uploading it to the Cloud) your data to yourself with a fully-homomorphic encryption scheme (in that you hold the private key yourself). Then, the Cloud service, which cannot decrypt those ciphertexts, runs the computation on the encrypted data (using, possibly many, homomorphic addition and homomorphic multiplication operations) and ultimately sends back the encrypted result, which only you can decrypt.
4.1 Threshold FHE and Multi-Key FHE
Two variants of FHE are suitable for multi-party settings. In Threshold FHE (Asharov et al., 2011) there is common public key, and a secret key that is secret-shared among multiple parties. The parties can collaboratively decrypt the ciphertext without learning anything beyond the plaintext.
Multi-Key FHE (MK-FHE) enables homomorphic operations between ciphertexts that are encrypted under different keys. A MK-FHE ciphertext can be decrypted collaboratively by all parties that provided input ciphertexts.
Both schemes can in principle be used to achieve constant-round MPC schemes in which the communication complexity is only proportional to the input and output size, and independent of the circuit size.
MPC based on threshold and multi-key FHE schemes, however, is still an active area of re- search; an example of the state of the art is this article by Chowdhury et al.
4.2 Implementations
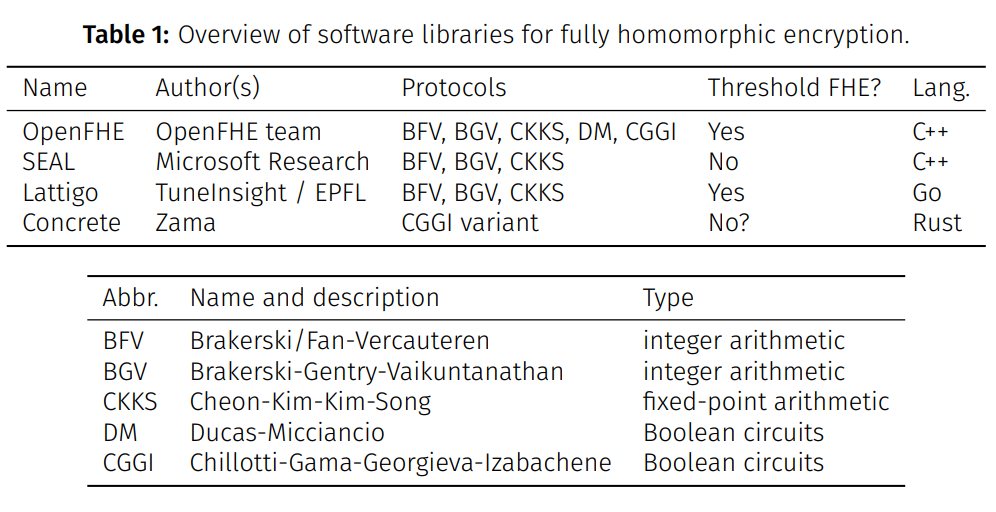
Several open-source FHE libraries exist, most notably:
- OpenFHE library, a very recent library and a combined effort by authors of several older FHE libraries like PALISADE, HElib, HEAAN, and FHEW;
- Microsoft SEAL by Microsoft Research;
- Lattigo by EPFL and TuneInsight;
- Concrete by Zama.
In Table 1, we compare those libraries qualitatively. There, you will also find a legend for the protocol abbreviations.
4.3 Programmability
Although developing software with FHE remains complex, certain recent innovations reduce this complexity.
Traditionally, as an FHE-application programmer, one had to keep track of “ciphertext noise”, which grows with the number of homomorphic operations; if this noise becomes too large, one cannot decrypt the ciphertext anymore. While it is beyond the scope of this write up to explain where this noise comes from, it suffices to know that in case of larger computations, one needed (or needs, depending on the FHE library) to repeatedly apply a so-called “bootstrap” procedure (after every k homomorphic operations on the same ciphertext, for some fixed k), which lowers the ciphertext noise. Bootstrapping is typically a performance bottleneck of FHE-based computation. Also, certain operations are significantly faster in particular FHE schemes, which creates the need for switching between FHE schemes during a larger computation, further adding to the complexity. Newer FHE libraries (e.g., OpenFHE) can keep track of the noise and can automatically apply bootstrapping as well as scheme-switching.
Another development worth mentioning is the advent of FHE-transpilers. A transpiler, some- times called a source-to-source compiler, is a tool that translates source code written in one programming language into equivalent source code in another programming language. For ex- ample, Google has made an experimental FHE-transpiler that can translate a program written in a restricted subset of C++ into an equivalent program that executes the original program logic ho- momorphically on FHE-encrypted inputs. While promising, the combination of current transpilers and FHE libraries do not yet yield production-grade results, as also indicated by the following dis- claimer from Google’s FHE C++ Transpiler:
This is currently an exploratory proof-of-concept. While it could be deployed in practice, the run-times of the FHE-C++ operations are likely to be too long to be practical at this time.
4.4 Performance
FHE is computationally very expensive; according to Feldmann et al. (2021) and when using a software-based FHE implementation, FHE is “[…] four to five orders of magnitude slower than computing on unencrypted data.” On of Microsoft SEAL’s contributors (Wei Dai) wrote in April 2020:
Homomorphic encryption is not a generic technology: only some computations on encrypted data are possible. It also comes with a substantial performance overhead, so computations that are already very costly to perform on unencrypted data are likely to be infeasible on encrypted data. Moreover, data encrypted with homomorphic encryption is many times larger than unencrypted data, so it may not make sense to encrypt, e.g., entire large databases, with this technology. [. . .]
On the other hand, there has been enormous progress since Gentry’s FHE scheme, improving the performance. Initiatives exist to accelerate homomorphic encryption using optimized software libraries (like Intel HEXL) or hardware accelerators, like ASICs or FPGAs. FHE is traditionally viewed as being “compute-bound” (which means that the primary performance bottleneck is the speed at which the system performs computations). In the presence of hardware accelerators, FHE becomes “memory-bound” (primary performance bottleneck is the memory bandwidth), because of the large sizes of the ciphertexts. The main problem with relying on accelerators, however, is that those accelerators are not available in today’s Cloud environments, posing a major deployment problem.
5. Secure Multi-Party Computation
The goal of secure multi-party computation (MPC) is for multiple parties to collaboratively evaluate a function on multiple inputs (originating from multiple parties) such that the result is correctly computed, the result is revealed to a designated subset of parties, and without revealing any information beyond this (in particular, the parties cannot see each other’s inputs).
We can achieve the above goal by means of implementing (typically, in software) an MPC protocol. When comparing different flavours of MPC protocols, it helps to distinguish between two-party computation and multiparty computation involving more than two parties. Three main flavours of MPC exist: MPC based on garbled circuits (GC), MPC based on arithmetic secret sharing and MPC based on a threshold or multi-key homomorphic encryption scheme.
5.1 Garbled Circuits
Garbled circuits, introduced by Yao (1986), allow two parties to evaluate Boolean circuits in MPC (although there exist both multi-party as well as arithmetic-circuit extensions for GC, we do not discuss such extensions here). In GC-based MPC, the two parties respectively assume the role of the garbler and the evaluator.
The garbler first prepares a so-called garbled circuit, which is a Boolean circuit that is “encrypted” in the following sense. First, each wire (carrying a binary value) is labeled with two randomly generated keys (the wire-value keys) corresponding to, respectively, a zero and a one. Then, the output column of each row of the truth table of each Boolean gate is encrypted with a symmetric encryption scheme, such that the wire-value key of the gate’s output is encrypted under the concatenation of the corresponding input wire-value keys.
Then, the garbler sends the garbled circuit to the evaluator. The evaluator starts with the right wire-value-keys corresponding to the leaves of the circuit, and to her private input. (Note that the evaluator obtains these initial keys from the garbler without revealing her input via a cryptographic primitive known as oblivious transfer.) The evaluator can decrypt gates one-by- one, every time obtaining new keys with which she can decrypt the next gate(s), up until the wire-value key corresponding to the result of the function. Finally, depending on who may learn the result, either the garbler sends the mapping between those final wire-value keys and the corresponding bits to the evaluator, or the evaluator sends the final wire-value key to the garbler.
Garbled circuits in the above sense provide passive security; the standard trick to turn this into an actively secure two-party MPC protocol is by applying the “cut-and-choose” technique: the garbler sends many independent copies to the evaluator, who opens a random subset of these circuits to check that the garbler is not cheating by preparing incorrect circuits.
An advantage of GC is that interaction between the parties only takes place at the beginning and the end of the computation; no interaction is needed during the computation. Potential disadvantages are, with respect to computations involving integer arithmetic, the corresponding Boolean circuit (hence, the garbled circuit) might become rather large, and note that this garbled circuit must be communicated to the evaluator.
Another fact is that GC relies on oblivious transfer, meaning that there is some underlying cryptographic assumption. Performance-wise, OT is not a bottleneck anymore because of mature OT-extension techniques (the line of research initiated by Ishai, et al. (2003).
5.1.1 Implementation aspects
Using garbled circuits requires a circuit compiler that compiles a function into a Boolean circuit. Tools for this purpose include EMP-toolkit and CBMC-GC. In early GC implementations, the entire circuit needed to fit in memory, which was a bottleneck. In modern implementations, however, the garbled circuit is generated on-the-fly and is sent as a stream to the evaluator.
Existing GC libraries include CRGC, EMP SH2PC and TinyGarble2.
5.1.2 Further reading
For a good overview of the state of the art of garbled-circuits MPC, we recommend a A Pragmatic Introduction to Secure Multi-Party Computation by Evans et al.
5.2 MPC based on Arithmetic Secret Sharing
A (t, n) threshold secret sharing scheme lets us convert a secret value s (from some finite ring or finite field) into a list of n shares with the following property: any collection of up to t shares reveals no information about the secret s, while any t + 1 shares determine the secret. Now suppose that we distribute the shares over n parties by giving each party one share. Effectively, we have shared the secret s over these n parties: t+1 parties could gather and use the reconstruction functionality of the secret sharing scheme to reconstruct the secret.
By taking a linear secret sharing scheme, n parties could perform addition of two secret- shared values non-interactively, by locally adding the corresponding shares. Using a slightly more complicated protocol that depends on the secret-sharing method, and which also involves interaction between the parties, they can perform a multiplication of two secret-shared values. The ability to perform addition and multiplication on secret shares enables the parties to securely evaluate any function represented in the form of an arithmetic circuit.
Well known examples of MPC protocols are the (passively secure) BGW protocol (Ben-Or et al., 1988) using Shamir secret sharing, and the (covertly or actively secure) SPDZ protocol (Smart et al., 2012).
5.2.1 Implementation Techniques
Most of the existing arithmetic-secret-sharing-based MPC frameworks use one of the following two implementation styles.
The first style exposes the MPC framework as a library; the programmer writes the program in a some existing host language (e.g., C or Python), and calls library functions. Using those library functions, the programmer dynamically instantiates the arithmetic circuit, corresponding to the MPC protocol, in the form of a task graph. The VIFF framework (and its descendants) are an example of this style.
The other style uses a domain-specific-language (DSL), i.e., a programming language for directly specifying multi-party computations. This DSL-code is then translated into bytecode (via a DSL-to-bytecode compiler), and executed by a virtual machine. The Bristol-SPDZ framework is an example of this style of implementation. A potential issue of the DSL-implementation-style is that writing a robust DSL compiler is a huge engineering effort in itself. Indeed, in many DSL-based MPC frameworks, the tailor-made compiler is rather immature and typically becomes a bottleneck when implementing protocols that have complex structure, or protocols that operate on large amounts of data.
5.2.2 The Outsourcing Scenario
In practical deployments of MPC, there may be parties who merely provide input and/or consume output, but do not participate in the actual computation (e.g., because they cannot run a server). This setting is known in the MPC literature as the outsourcing scenario, because the computation is outsourced to the compute parties, i.e. those parties that participate in the multi-party computation. We briefly mention this setting here, because it is a practical approach to consume input from (and/or deliver output to) many parties while keeping the number of protocol parties low, which is a benefit for efficiency and performance.
5.2.3 Performance
MPC incurs a significant performance overhead when compared to ordinary computation; this overhead mainly stems from the need for interaction between the parties during the computation. Hence, the performance is strongly influenced by the latency and throughput of the network. On the other hand, the computational overhead is (much) lower than fully homomorphic encryption.
The overhead depends on the MPC protocol that is used, and strongly depends on whether the protocol offers passive or active security, and whether the protocol offers its security guarantees in the presence of an honest majority of parties, or also in case the majority of parties is dishonest.
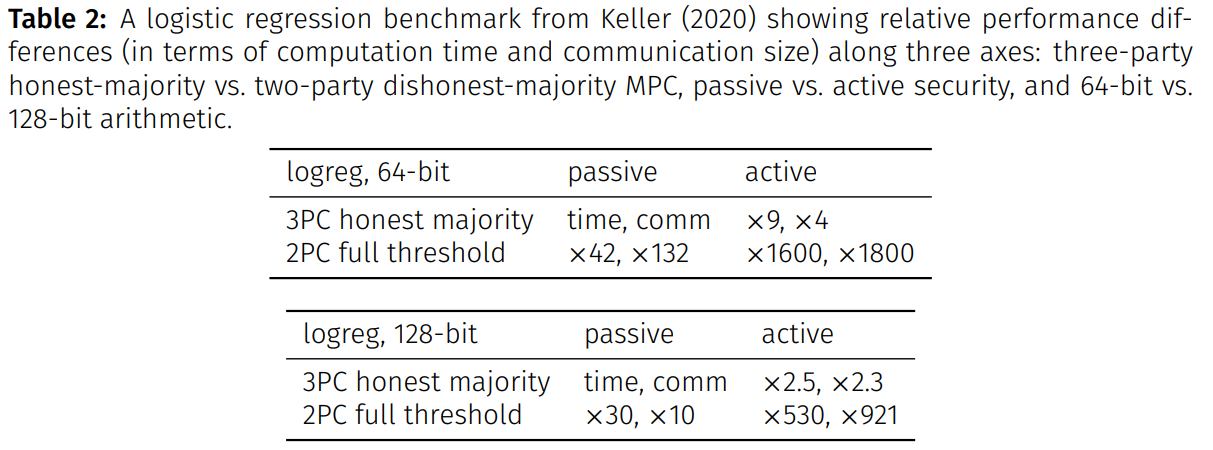
Keller gives an extensive performance comparison between different MPC protocols. In particular, the paper presents a logistic regression benchmark that gives a ballpark estimate for the relative performance differences between three-party honest-majority MPC (passive as well as active security) and two-party dishonest-majority (full threshold) MPC (passive and active). Table 2 shows these relative differences, in terms of computation time and communication size.
5.2.4 Further reading
We refer the reader to “An Introduction to Secret-Sharing-Based Secure Multiparty Computation” by Escudero, and to Secure Multiparty Computation and Secret Sharing by Cramer et al.
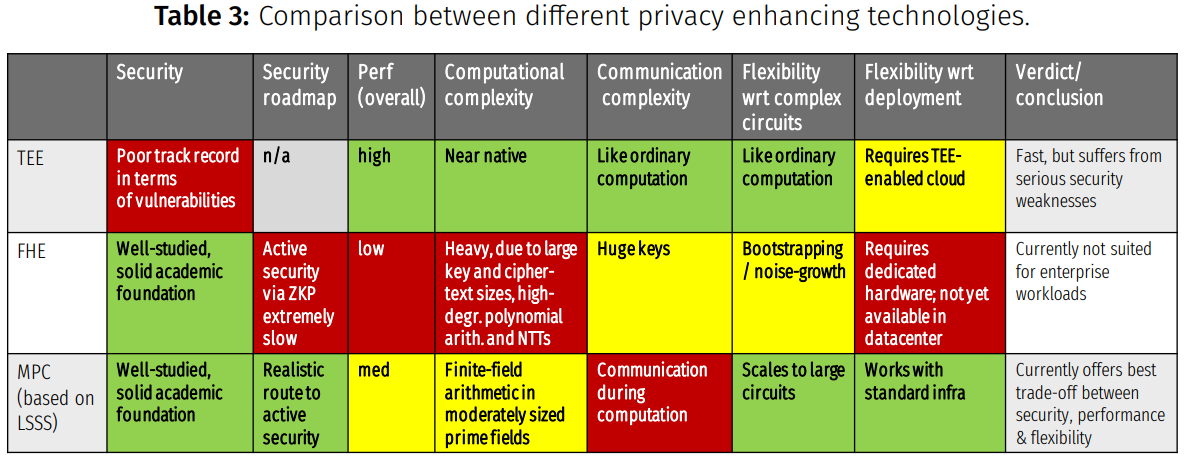
6. Side-by-Side Comparison
In Table 3, we show a qualitative comparison between trusted-execution environments, fully homomorphic encryption, and (arithmetic-secret-sharing-based) secure multiparty computation. We compare along several categories, we describe each of them below.
Security General: Remarks with respect to security foundations and/or known problems;
Security roadmap: Most practical PET solutions currently offer passive security; how realistic is a transition to active security?
Performance: Rough and relative (qualitative) indication of the overall runtime performance;
Computational complexity: How much computational overhead does the technology induce, when compared to ordinary (cleartext) computation?
Communication complexity: Relative comparison in terms of the amount of data that needs to be communicated between parties; and, does the method require interaction during computation, or only at the beginning and the end?
Flexibility with respect to complex circuits: How does the technology cope with complex (deep) circuits?
Flexibility with respect to deployment: Can the technology be deployed on any hardware, or is dedicated hardware like accelerators required for its operation?
6.1 Our Rationale for Adopting MPC
Roseman Labs uses secure MPC as its main privacy technology, because we are convinced that MPC currently has the best overall “scorecard,” when taking security, runtime performance, and versatility into account.
In some more detail, and in addition to the above comparison, the MPC scheme that we currently use (BGW) enjoys information-theoretic security (hence, we do not rely on less well-studied computational intractability assumptions; but note that we do rely on standard public-key cryptography for establishing secure channels). Furthermore, the secret-sharing technique (Shamir) does not have significant ciphertext expansion: secret sharing one field element (the value) gives rise to one field element (a share) per party. Protocols for basic arithmetic are straightforward to implement and can be made highly efficient.